Lecture 5¶
Equivalence of CFG and PDA¶
Theorem
CFG and PDA are equivalent.
- \(\forall \text{ PDA } M, \exist \text{ CFG } G,\ s.t.\ L(M) = L(G).\)
- \(\forall \text{ CFG } G, \exist \text{ PDA } M,\ s.t.\ L(G) = L(M).\)
Proof
CFG \(\Rightarrow\) PDA.
\(\forall G = (V, \Sigma, S, R)\), we construct a PDA \(M = (K, \Sigma, \Gamma, \Delta, s, F)\), where
- \(\Gamma = V\),
- \(K = \{s, f\}\),
- \(F = \{f\}\),
-
transition relation
\[ \begin{aligned} \Delta = \{ & ((s, e, e), (f, S)), \\ & ((f, e, A), (f, u)) \text{ for each } (A, u) \in R, \\ & ((f, a, a), (f, e)) \text{ for each } a \in \Sigma \} \end{aligned} \]
PDA \(\Rightarrow\) CFG.
First we define simple PDA.
A PDA \(M = (K, \Sigma, \Gamma, \Delta, s, F)\) is simple if
- \(|F| = 1\),
- For each transition \(((p, a, \alpha), (q, \beta)) \in \Delta\),
- either \(\alpha = e\) and \(|\beta| = 1\),
- or \(|\alpha| = 1\) and \(\beta = e\).
For any PDA \(M\), we first transform it to a corresponding simple PDA \(M' = (K, \Sigma, \Gamma, \Delta', s, F')\),
- If \(|F| > 1\), we create a new state \(f'\). For each \(q \in F\), we add a new transition \(((q, e, e), (f', e))\) and set \(F' = \{f'\}\).
-
For each transition \(\delta \in \Delta\), if it's not satifsying the condition of simple PDA, then it only be of the following four cases.
- 2.1 \(|\alpha| \ge 1\) and \(|\beta| \ge 1\).
- 2.2 \(|\alpha| \ge 1\) and \(\beta = e\).
- 2.3 \(\beta = e\) and \(|\beta| \ge 1\).
- 2.4 \(\alpha = e\) and \(\beta = e\).
For 2.1 \(((p, a, \alpha), (q, \beta))\), create a new state \(r\) and replace it with \(((p, a, \alpha), (r, e))\) and \(((r, e, e), (q, \beta))\), which comes to 2.2 and 2.3.
For 2.2 \(((p, a, \alpha), (q, e))\), supposing \(\alpha = c_1 c_2 \cdots c_k\), create new states \(r_1, \dots, r_k\) and replace it with
\[ ((p, a, c_1), (r_1, e)), ((r_1, e, c_2), (r_2, e)), \dots ((r_{k - 1}, e, c_k), (q, e)). \]For 2.3, similar to 2.2.
For 2.4 \(((p, a, e), (q, e))\), create a new state \(r\), pick some \(c \in \Gamma\), and replace it with \(((p, a, e), (r, c))\) and \(((r, e, c), (q, e))\).
Now that we have a simple PDA \(M' = (K, \Sigma, \Gamma, \Delta', s, F')\) from the PDA \(M\), we construct a CFG \(G = (V, \Sigma, S, R)\).
We define the non-terminal \(V - \Sigma = \{A_{pq} | \text{ for } p, q \in k\}\). And we claim that
Then \(S = A_{sf}\). And we construct the rules \(R\) by
- \(\forall p \in K\), \(A_{pp} \rightarrow e\).
- \(\forall p, q \in K\),
- \(A_{pq} \rightarrow A_{pr}A_{rq}, \forall r \in K\).
- \(A_{pq} \rightarrow a A_{p'q'} b, \forall ((p, a, e), (p', \alpha)) \in \Delta, ((q', b, \alpha), (q, e)) \in \Delta\) for some \(\alpha \in \Gamma\).
Then for the claim before,
- \(\Rightarrow\) : by induction on length of derivation from \(A_{pq}\) to \(w\).
- \(\Leftarrow\) : by induction on the number of steps of the computation.
Since the equivalence of PDA and CFG, we can use PDA to define context-free language. Since NFA is a subset of PDA, so regular language is a subset of context-free language.
Theorem
Every regular language is context-free.
Closure Property¶
Similar to regular language, we have context-free language properties closure.
Theorem
If \(A\) and \(B\) are context-free, so is \(A \cup B\), \(A \circ B\) and \(A^*\). But NOT \(A \cap B\) and \(\overline{A}\).
Proof
For CFG \(G_A = (V_A, \Sigma, S_A, R_A)\) and \(G_B = (V_B, \Sigma, S_B, R_B)\), then
- \(G_{A \cup B} = (V_A \cup V_B, \Sigma, S, R_A \cup R_B \cup \{S \rightarrow S_A | S_B\})\).
- \(G_{A \circ B} = (V_A \cup V_B, \Sigma, S, R_A \cup R_B \cup \{S \rightarrow S_AS_B\})\).
- \(G_{A^*} = (V_A, \Sigma, S, R_A \cup \{S \rightarrow e\} \cup \{S \rightarrow SS_A\})\).
One counter example of \(A \cap B\) and \(\overline{A}\) is \(A = \{a^i b^j c^k | i = j\}\) and \(B = \{a^i b^j c^k | j = k\}\). Both \(A\) and \(B\) are context-free, but \(A \cap B = \{a^nb^nc^n | n \ge 0\}\) is not context-free (we will prove it later after giving pumping theorem for CFL).
Since \(A \cap B = \overline{\overline{A} \cup \overline{B}}\), we can show that \(\overline{A}\) is not context-free.
Pumping Theorem¶
Pumping Theorem for CFL
Let \(L\) be a context-free language. There exists an integer \(p \ge 1\) such that any \(w \in L\) with \(|w| \ge p\) can be divided into \(w = uvxyz\), where
- for each integer \(i \ge 0\), \(uv^ixy^iz \in L\).
- \(|v| + |y| > 0\).
- \(|vxy| \le p\).
We call the value \(p\) pumping length.
NOTE This theorem is a necceasry condition of regular language but not sufficient.
Proof
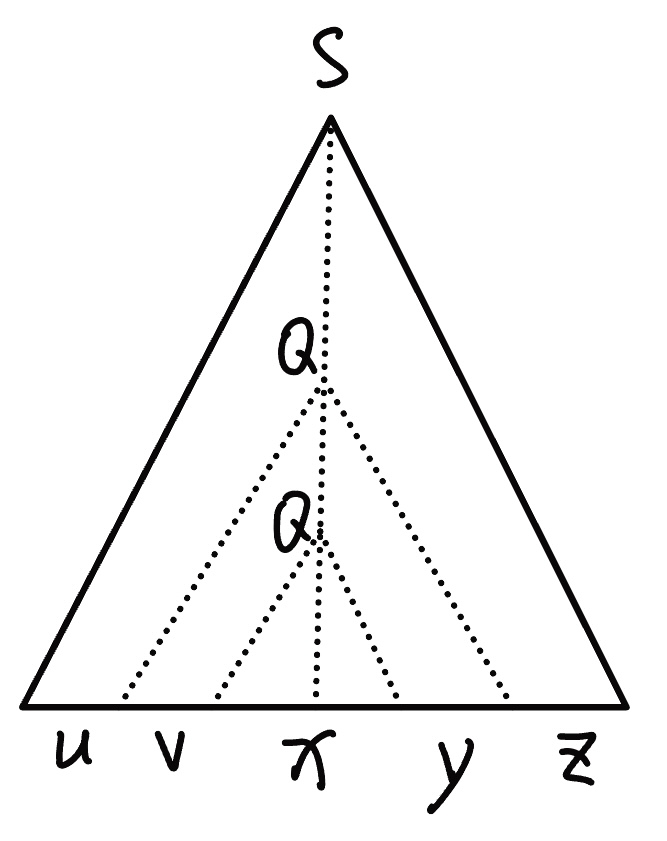
Since \(L\) is context-free, there exists a CFG \(G = (V, \Sigma, S, R)\) with \(L(G) = L\). Let \(b = \max\{|u| : (A, u) \in R\}\), namely the largest fanout (the number of children) of nodes in the parse tree.
If a tree with fanout less than or equal \(b\) has \(n\) leaves, then its height \(h \ge \log_b n\).
Let \(p = b^{|V - \Sigma| + 1}\), for any \(w \in L\) with \(|w| \ge p\). Let \(T\) be the parse tree of \(w\) with smallest number of nodes, and the height of \(T\) is \(h \ge \log_b p = |V - \Sigma| + 1\).
Since the length of the longest path from the root of the parse tree to its leaves is \(|V - \Sigma| + 1\), with the number of nodes \(|V - \Sigma| + 2\). Namely the number of non-terminals along the path is \(|V - \Sigma| + 1\). Thus there must be some non-terminal \(Q\) that appears twice along the path.
From the graph of parse tree, we can derive
- for each integer \(i \ge 0\), \(uv^ixy^iz \in L\).
- if \(v = y = e\), then there exists a parse tree smaller than \(T\), which leads to a contradiction. Thus \(|v| + |y| > 0\).
- for the subtree with root \(Q\), its height \(h' \le |V - \Sigma| + 1\), thus \(|vxy| = \# \text{leaves} \le b^{|V - \Sigma| + 1} = p\).
Example
Show that \(L = \{a^nb^nc^n | n \ge 0\}\) is not context-free.
Proof
Assume \(L\) is context-free. Let \(p\) be the pumping length given by the pumping theorem. Then \(\forall w \in L, |w| \ge p\), or particularly, we let \(w\) be
Then \(w\) can be written as \(w = uvxyz\), such that
- \(uv^ixy^iz \in L\) for any \(i \in \mathbb{N}\).
- \(|v| + |y| > 0\).
- \(|vxy| \le p\).
From 2. and 3., we can infer there will be three cases.
- \(|vxy| = b^p\).
- \(|vxy| = a^{p - k}b^k\) for some for some integer \(1 \le k \le p\).
- \(|vxy| = b^{p - k}c^k\) for some for some integer \(1 \le k \le p\).
However, in all these three cases, \(uv^0xy^0z \notin L\), which leads to a contradition with 1.
创建日期: 2023.10.30 11:18:07 CST