Chapter 10 | Graphs¶

Definition

A simple graph $G = (V, E)$ consists of $V$, a nonempty set of vertices and $E$, a set of unordered pair of distinct elements of $V$ called edges.
A multigraph $G = (V, E)$ consists of $V$, $E$ and a function from $E$ to $\{\{u, v\} | u, v \in V, u \neq v\}$. The edges $e_1$ and $e_2$ are called multiple or parallel edges if $f(e_1) = f(e_2)$.
A pseudograph $G = (V, E)$ consists of $V$, $E$ and a function from $E$ to $\{\{u, v\} | u, v \in V\}$. An edge is a loop if $f(e) = \{u, u\} = \{u\}$ for some $u \in V$.
A directed graph $G = (V, E)$ consists of $V$, and a set of edges $E$ that are ordered pairs of elemetnes of $V$.
A directed multigraph $G = (V, E)$ consists of $V$, $E$ and a function from $E$ to $\{(u, v) | u, v \in V, u \neq v\}$. The edges $e_1$ and $e_2$ are called multiple or parallel edges if $f(e_1) = f(e_2)$.

Type	Edges	Multiple Edges?	Loop?
Simple Graph	Undirected	No	No
Multigraph	Undirected	Yes	No
Pseudograph	Undirected	Yes	Yes
Directed Graph	Directed	No	Yes
Directed multigraph	Directed	Yes	Yes

Definition

$H$ is a subgraph of $G$, if $W \subseteq V,\ \ F \subseteq E$.
$H$ is a spanning subgraph of $G$, if $W = V,\ \ F \subseteq E$.
Union of two simple graph $G_1 = (V_1, E_1)$ and $G_2 = (V_2, E_2)$ is the simple graph with vertex set $V_1 \cup V_2$ and edge set $E_1 \cup E_2$, denoted by $G_1 \cup G_2$.

Adjacency and Degree¶

Tip

In undirected graph, we use $\{u, v\}$ to denote an edge, while in directed graph, we use $(u, v)$ to denote an edge.

Definition

For Undirected graph,

$u$ and $v$ are adjacent or neighbours if $e = \{u, v\}$ is an edge of $G$.
- $e$ is incident with $u$ and $v$.
- $u$ and $v$ are endpoints.
The degree of a vertex is the number of edges incident with it, except that a loop at a vertex contribute twice to the degree, denoted by $\text{deg}(v)$.
- Isolated vertex: $\text{deg} = 0$.
- Pendant vertex: $\text{deg} = 1$.

Theorem | Handshaking Theorem

$G$ is a graph with $n$ vertices $v_1, v_2, \cdots, v_m$ and $m$ edges, then

\[ \sum\limits_{i = 1}^{n} \text{deg}(v_i) = 2m. \]

Definition

For a directed graph,

If $e = (u, v)$ is an edge of $G$.
- $u$ is the initial vertex and adjecnt to $v$.
- $u$ is the end vertex or terminal and adjecnt from $v$.
In-degree of $v$, denoted by $\text{deg}^{-}v$, is the number of edges with $v$ as their end vertex.
Out-degree of $v$, denoted by $\text{deg}^{+}v$, is the number of edges with $v$ as their initial vertex.

Theorem

$G$ is a directed graph,

\[ \sum\limits_{i = 1}^{n} \text{deg}^{-}(v_i) = \sum\limits_{i = 1}^{n} \text{deg}^{+}(v_i) = |E|. \]

Special Simple Graphs¶

Complete Graph $K_n$

The complete graph $K_n$ is the simple graph with $n$ vertices and every pair of vertices is joined by an edge.

\[ K_n = (V, E),\ \ \text{ where } E = \{\{u, v\} | u \ne v\}. \]

Remark $|E| = C(n ,2)$.

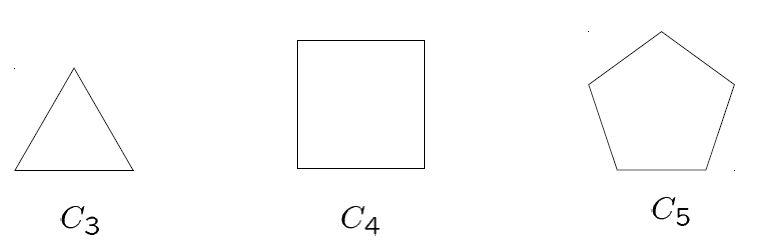
Cycles $C_n$

The cycle $C_n$ ($n ge 3$) consists of $n$ vertices $v_1, v_2, \dots, v_n$ and edges $\{v_1, v_2\}, \{v_2, v_3\}, \dots \{v_{n - 1}, v_n\} and \{v_n, v_1\}$.

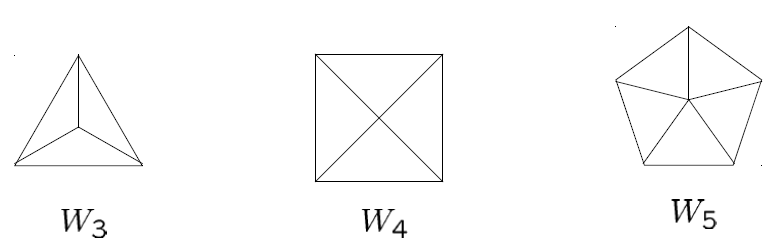
Wheels $W_n$

The wheel $W_n$ is to add an additional vertex to the cycle $C_n$, and connect this new vertex to each of $n$ vertices by new edges.

n-Cubes $Q_n$ n 维超立方体

n-Cubes $Q_n$ is the graph has vertices representing $2^n$ bit strings of length $n$.

Bipartite Graph 二分图 / 偶图

A bipartite graph $G = (V, E)$ is a graph s.t.

\[ V = V_1 \cup V_2,\ \ V_1 \cap V_2 = \emptyset. \]

and no edges between any two vertices in the same subset $V_k$ ($k = 1, 2$).

A bipartite graph is the complete bipartite graph $K_{m, n}$ if every vertex in $V_1$ is joined to a vertex in $V_2$ nad conversely, and $|V_1| = m$, $|V_2| = n$.

Representation¶

There are many ways to represent graphs: Graph, adjacecy lists, adjacency matrices and incidences.

Adjacency Matrix 邻接矩阵¶

Definition

$G$ is a graph, then its corresponding adjacency matrix $A = [a_{ij}]_{n \times n}$ where

$G$ is a simple graph, then

\[ a_{ij} = \left\{ \begin{aligned} & 1, & \{v_i, v_j\} \in E, \\ & 0, & \text{otherwise}. \end{aligned} \right. \]
$G$ is a pseudograph, then

\[ a_{ij} = \text{the number of edges that are associated to } \{v_i, v_j\}. \]
$G$ is a directed graph, then

\[ a_{ij} = \left\{ \begin{aligned} & 1, & (v_i, v_j) \in E, \\ & 0, & \text{otherwise}. \end{aligned} \right. \]
$G$ is a directed multigraph, then

\[ a_{ij} = \text{the number of edges that are associated to } (v_i, v_j). \]

Property

The adjacency matrix of an undirected graph is symmetric, $a_{ij} = a_{ji}$.
For simple graph,
- $a_{ii} = 0$ since a simple graph has no loops.
- $\text{deg}(v_i) = \sum\limits_{j = 1}^{n} a_{ij}$.

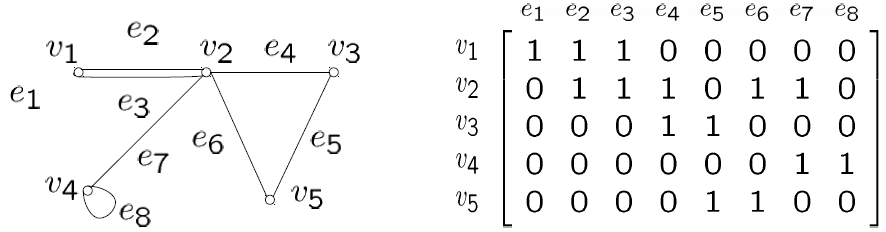
Incidence Matrix 关联矩阵¶

Definition

$G = (V, E)$ is an undirected graph with vertices $v_1, \dots, v_n$ and edges $e_1, \dots, e_n$, then the incidence matrix w.r.t this ordering of $V$ and $E$ is matrix $M = [m_{ij}]_{n \times m}$, where

\[ m_{ij} = \left\{ \begin{aligned} & 1, & \text{when edge $e_j$ is incidence with $v_i$}, \\ & 0, & \text{otherwise}. \end{aligned} \right. \]

Example

Isomorphism of Graphs¶

Definition

Two simple graphs $G_1 = (V_1, E_1)$ and $G_2 = (V_2, E_2)$ are called isomorphic, if there is a bijection $f$ from $V_1$ to $V_2$ with the property

\[ \forall\ a, b \in V_1,\ \ (a, b) \in E_1 \Leftrightarrow (f(a), f(b)) \in E_2. \]

Bijection $f$ is called an isomorphism.

Connectivity¶

Definition

Similarly we defines path, circuit, simple path / circuit, connection, connected components, cut vertices / point, cut edge / bridge, strongly connected and weakly connected.

Refer to Graph.

Theorem

There are a simple path between every pair of distinct vertices of a connected undirected graph.

Theorem

$G$ is a graph with its adjacency matrix $A$ w.r.t the ordering $v_1, \dots, v_n$. The number of different paths of length $r$ from $v_i$ to $v_j$ equals to the $(i, j)$th entry of $A^r$.

Note

We can use this theorem to determine whether a graph is connected.

Euler Paths and circuits¶

Definition

An Euler Path is a simple path containing every edge of $G$.
An Euler Circuit is a simple circuit containing every edge of $G$.
A graph $G$ is an Euler graph if it has an Euler circuit.

Theorem

A connected multigraph $G = (V, E)$ has an Euler curcuit iff every vertex has even degree.

Hamilton Paths and circuits¶

Definition

An Hamilton Path is a path go through all vertices.
An Hamilton Circuit is a circuit go through all vertices.
A connected graph $G$ is an Hamilton graph if it has an Hamilton circuit.

Theorem

A connected simple graph $G$ with $n$ ($n \ge 3$) vertices has a Hamilton circuit if the degree of each vertex is at least $n / 2$.

Theorem

A connected simple graph $G(V, E)$ with $n$ ($n \ge 3$) vertices has a Hamilton circuit if

\[ \forall u, v \in V,\ \ d(u) + d(v) \ge n. \]

Shortest Path Problems¶

Refer to Shortest Paths.

Planar Graphs¶

Definition

A graph is called planar if it can be drawn in the plane without crossing edges. Such a drawing is called a planar representation of the graph.

Example

$K_4$ is planar, $Q_n$ is all planar. But $K_5$ and $K_{3,3}$ are not planar.

Definition

A planar representation of a graph into regions, including an unbounded region.

Theorem | Euler's Formula

Let $G$ be a connected planar simple graph with $e$ edges and $v$ vertices. Let $r$ be the number of regions in a planar representation of $G$. Then

\[ v - e + r = 2. \]

Further consider the conditions of simple and connected.

If not simple, we still have $v - e + r = 2$.
If not connected, but $n$ connected components instead, then we have

\[ v - e + r = n + 1. \]

From Euler's Formula, some corollaries are derived to easily show a graph is nonplanar.

Corollary

If $G$ is a connected planar simple graph with $e$ edges and $v$ vertices ($v \ge 3$), then

\[ e \le 3v - 6. \]

If $G$ is a connected planar simple graph with $e$ edges and $v$ vertices ($v \ge 3$), and no circuits of length $3$, then

\[ e \le 2v - 4. \]

NOTE: the condition simple is neccessary.

Proof

Define degree of a region is the number of edge on the boundary of the region.

Since it's a simple graph, the degree of each region is at least $3$.
And the degree of the unbounded region is at least $3$.

Thus

\[ 2e = \sum\limits_{\text{all region $R$}}\text{deg}(R) \ge 3r \Rightarrow \frac{2}{3}e \ge r. \]

From Euler formula, we have

\[ e - v + 2 = r \le \frac{2}{3}e \Rightarrow e \le 3v - 6. \]

Example

Show that $K_5$ and $K_{3, 3}$ are nonplanar.

Proof

For $K_5$, $v = 5$, $e = 10$. Since

\[ 10 = e > 3v - 6 = 3 \times 5 - 6 = 9. \]

From the first corollary, $K_5$ is nonplanar.

For $K_{3,3}$, $v = 6$, $e = 9$. Since the circuits of $K_{3,3}$ is even length, thus at least $3$. And

\[ 9 = e > 2v - 4 = 2 \times 6 - 4 = 8. \]

From the first corollary, $K_{3,3}$ is nonplanar.

Furthermore, we have the sufficient and necessary condition of nonplanar graph. First we need some defintions.

Definition

$G = (V, E)$. Let $\{u, v\} \in E$. Elementary subdivision is the process that remove the edge $\{u, v\}$ and add new vertex $w$ together with edges $\{u, w\}$ and $\{w, v\}$.

Graphs $G_1 = (V_1, E_1)$ and $G_2 = (V_2, E_2)$ are called homeomorphic 同胚 if they can be obtained from the same graph by a sequence of elementary subdivision.

Kuratowski's Theorem

A graph $G$ is nonplanar iff $G$ contains a subgraph homeomorphic to $K_5$ or $K_{3,3}$.

Graph Coloring¶

Each map in the plane can be represented by a graph, by the following processes:

Each region of the map is represented by a vertex.
Edges connect two vertices if each regions represented by these vertices have a common border.

The graph is called dual graph of the map.

Definition

A coloring of a simple graph is the assignment of a color to each vertex of the graph so that no two adjectent vertices are assigned the same color.

The chromatic number of the graph is the least number of colors needed for a coloring of this graph.

The Four Color Theorem

The chromatic number of a planar graph is no greater than four.

Example

The chromatic number of $K_n$ is $n$.
The chromatic number of the complete bipartite $K_{m, n}$ is $2$. (it's also the sufficient and necessary condition)
The chromatic number of $C_n$ is n % 2 == 0 ? 2 : 3.

The best algorithms known for finding the chromatic number of a graph have exponential worst-case time complexity.

最后更新: 2023.11.21 17:00:13 CST
创建日期: 2022.11.10 01:04:43 CST