Chapter 9 | Relations¶

Definition

A binary relation $R$ between $A$ and $B$ is a subset of the Cartesian product $A \times B$.

\[ R \subseteq A \times B \]

when $A = B$, R is a relation on $A$.

The domain of $R$: $\text{Dom}(R) = \{x \in A | (x, y) \in R \text{ for some } y \in B\}$.
The range of $R$: $\text{Ran}(R) = \{y \in B | (x, y) \in R \text{ for some } x \in A\}$.

Property

There are $2^{n^2}$ relations on a set with $n$ elements.

Combining Relations¶

Since the nature of relation is a set, thus we have union, intersection, complement and difference. Moreover, we have composite.

Definition

Let $R$ be a relation from a set $A$ to $B$ and $S$ is a relation from $B$ to $C$. The composite of $R$ and $S$ is the relation

\[ S \circ R = \{(a, c) | a \in A, c \in C, \exist\ b \in B\ s.t.\ (a, b) \in R, (b, c) \in S\}. \]

Denote $R^1 = R,\ \ R^{n + 1} = R^n \circ R$.
Denote inverse $R^{-1} = \{(y, x) | (x, y) \in R\}$.

Properties¶

Definition

Let $R$ be a relation on a set $A$. Then

$R$ is reflexive $\Leftrightarrow$ $\forall\ x \in A, \ \ (x, x) \in R$.
$R$ is irreflexive $\Leftrightarrow$ $\forall\ x \in A, \ \ (x, x) \notin R$.

Remark

$R$ is reflexive iff $R_= \subseteq R$.
There are $2^{n(n - 1)}$ reflexive relations on a set with $n$ elements.

Definition

Let $R$ be a relation on a set $A$. Then

$R$ is symmetric $\Leftrightarrow$ $\forall\ x, y \in A,\ \ (x, y) \in R \Rightarrow (y, x) \in R$.
$R$ is antisymmetric $\Leftrightarrow$ $\forall\ x, y \in A,\ \ (x, y) \in R, (y, x) \in R \Rightarrow x = y$.

Remark

$R$ is symmetric iff $R^{-1} = R$.
$R$ is antisymmetric iff $R \cap R^{-1} \subseteq R_=$.
Non-symmetric is not the same as antisymmetric (e.g. $R_=$)
There are $2^{\frac{n(n + 1)}{2}}$ symmetric relations on a set with $n$ elements.
There are $2^{n} \cdot 3^{\frac{n(n - 1)}{2}}$ reflexive antisymmetric on a set with $n$ elements.

Definition

Let $R$ be a relation on a set $A$, then

$R$ is transitive $\Leftrightarrow$ $\forall x, y, z \in A, ((x, y) \in R \wedge (y, z) \in R) \Rightarrow (x, z) \in R$.

Remark

$R$ is transitive $\Leftrightarrow$ $R \circ R \subseteq R$.

Theorem

The relation $R$ on a set $A$ is transitive iff $R^n \subseteq R$ for $n = 2, 3, \dots$.

Representation¶

Matrix Form¶

Suppose $R$ is a relation from $A = \{a_1, a_2, \cdots, a_m\}$ to $B = \{b_1, b_2, \cdots, b_n\}$. The relation $R$ can be represented by matrix $M_R = (m_{ij})_{m \times n}$, where

\[ m_{ij} = \left\{ \begin{aligned} & 1, & (a_i, b_j) \in R \\ & 0, & (a_i, b_j) \notin R \\ \end{aligned} \right. \]

Property

$M_R^2$ = $M_R \circ M_R$.
$R$ is reflexive $\Leftrightarrow$ All terms $m_{ii}$ in the main diagnoal of $M_R$ are $1$.
$R$ is symmetric $\Leftrightarrow$ $m_{ij} = m_{ji}$ for all $i$ and $j$, namely a symmetric matrix.
$R$ is trasitive $\Leftrightarrow$ whenever $c_{ij}$ in $C = M_R^2$ is nonzero then entry $m_{ij}$ in $M_R$ is also nonzero. ($R^2 \subseteq R$)
Combining Relations

\[ M_{R_1 \cup R_2} = M_{R_1} \vee M_{R_2},\ \ M_{R_1 \cap R_2} = M_{R_1} \wedge M_{R_2},\ \ M_{S \circ R} = M_R \times M_S. \]

Graph Form¶

Each order pair is represented using an arc with its direction indicated by an arrow, thus we can use digraph to represent a relation.

Property

$R$ is reflexive $\Leftrightarrow$ There are loops at each vertex.
$R$ is symmetric $\Leftrightarrow$ Each edge is accompanied by an inverse edge.

Closures of Relations¶

Definition

Let $R$ be a relation on a set $A$. If there is a relation $S$ satisfying

$S$ with property $\textbf{P}$ (reflexive, symmetry, or transitivity).
$\forall\ S'$ with property $\textbf{P}$ and $R \subseteq S'$, then $S \subseteq S'$.

Then $S$ is called a closure of $R$ w.r.t. $\textbf{P}$.

Theorem

Let $R$ be a relation on a set $A$.

Reflexive closure of relation $R$:

\[ r(R) = R \cup \Delta. \]

where $\Delta = \{(a, a) | a \in A\}$ is diagonal relation on $A$.
Symmetric closure of relation $R$:

\[ s(R) = R \cup R^{-1}. \]
Transitive closure of relation $R$:

\[ t(R) = R^*,\ \ \text{ where $R^*$ is connectivity relation}. \]

Method to Find Transitive Closure¶

To find the transitive closure, we gives the following definition and theorem.

Theorem

Let $R$ be a relation on set $A$. There is a path of length $n$ from $a$ to $b$ $\Leftrightarrow$ $(a, b) \in R^n$.

Definition

The connectivity relation $R^* = \{(a, b) | \text{there is a path from \(a$ to $b$}\}\).

\[ R^* = \bigcup\limits_{n = 1}^{\infty} R^n. \]

If $R$ is on set $A$ with $n$ elements, then

\[ R^* = \bigcup\limits_{i = 1}^{n} R^i. \]

Lemma

Let $A$ be a set with $n$ elements, and let $R$ be a relation on $A$. If there is a path in $R$ from $a$ to $b$, then there is such a path with length not exceeding $n$. Moreover, when $a \ne b$, if there is a path in $R$ from $a$ to $b$, then there is such a path with length not exceeding $n - 1$.

Theorem

$M_R$ is the 0-1 matrix of the relation $R$ on a set $A$ with $n$ elements, Then the 0-1 matrix of the transitive closure $R^*$ is

\[ M_{R^*} = M_R \vee M_R^2 \vee \cdots \vee M_R^n. \]

Example

Find 0-1 matrix of the transitive closure of the relation $R$ where

\[ M_R = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{bmatrix}. \]

Solution.

\[ M_{R^*} = M_R \vee M_R^2 \vee M_R^3 = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{bmatrix} \vee \begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{bmatrix} \vee \begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 0 \\ 1 & 1 & 1 \end{bmatrix}. \]

Computational complexity of this method is $(n - 1)n^2(2n-1)+(n-1)n^2 = O(n^4)$. Now we introduce an $O(n^3)$ method to solve out transtive closure.

Warshall's Algorithm

Definition

For a path $a, x_1, \dots, x_{m-1}, b$, the interior vertices are $x_1, \cdots, x_{m - 1}$.

Define

\[ \begin{aligned} W_0 &= M^R, \\ W_k &= \left[w_{ij}^{(k)}\right]_{n \times n}. \end{aligned} \]

where

\[ \begin{aligned} w_{ij}^{(k)} = \left\{ \begin{aligned} & 1, && \substack{ \text{there is a path from $v_i$ to $v_j$ s.t all the} \\ \text{interior vertices of the path are in the set $\tiny \{v_1, v_2, \cdots, v_k\}$,} } \\ & 0, && {\tiny\text{otherwise.}} \end{aligned} \right. \end{aligned} \]

And from definition we have

\[ W_n = M_{R^*}. \]

Lemma

\[ w_{ij}^{(k)} = w_{ij}^{(k - 1)} \vee \left(w_{ik}^{(k - 1)} \wedge w_{kj}^{(k - 1)}\right). \]

Method

Compute $M_{R^*}$ by computing $W_0 \rightarrow W_1 \rightarrow \cdots \rightarrow W_n = M_{R^*}$.

Example

Find transitive closure of

\[ M_R = \begin{bmatrix} 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix}. \]

Solution.

W0W1 / W2W3W4

\[ W_0 = M_R = \begin{bmatrix} 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix}. \]

Consider the entries of $1$ in the first row (14) and the first column (21, 31). Combine them with elimination of 1 and we get 24 and 34, and thus set

\[ w_{24}^{(1)} = w_{34}^{(1)} = 1. \]

\[ W_1 = W_2 = \begin{bmatrix} 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix}. \]

Consider the entries of $1$ in the second row (21, 23, 24) and the second column (none). Thus $W_2 = W_1$.
Consider the entries of $1$ in the third row (31, 34) and the third column (23, 43). Combine them with elimination of 3 and we get 21, 24, 41 and 44, and thus set

\[ w_{21}^{(3)} = w_{24}^{(3)} = w_{41}^{(3)} = w_{44}^{(3)} = 1. \]

\[ W_3 = \begin{bmatrix} 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 \end{bmatrix}. \]

Consider the entries of $1$ in the fourth row (41, 43, 44) and the fourth column (14, 24, 34, 44). Combine them with elimination of 4 and we get 11, 13, 14, 21, 23, 24 and 31, 33, 34, and thus set

\[ \begin{aligned} w_{11}^{(4)} = w_{13}^{(4)} = w_{14}^{(4)} = 1. \\ w_{21}^{(4)} = w_{23}^{(4)} = w_{24}^{(4)} = 1. \\ w_{31}^{(4)} = w_{33}^{(4)} = w_{34}^{(4)} = 1. \end{aligned} \]

\[ M_{R^*} = W_4 = \begin{bmatrix} 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 1 \end{bmatrix}. \]

Equivalence Relations¶

Definition

Relation $R_\sim : A \leftrightarrow A$ is an equivalence relation if it's reflexive, symmetric and transitive.

Definition

Let $R: A \leftrightarrow A$ is an equivalence relatiion. For any $a \in A$, the equivalence class of $a$ is the set of the elements related to $a$, denoted by

\[ [a]_R = \{x \in A | (x, a) \in R\}. \]

If $b \in [a]_R$, then $b$ is called a representitive of this equivalence class.

Property

$\forall a \in A,\ \ a \in [a]_R \neq \emptyset.$
$(a, b) \in R \Rightarrow [a]_R = [b]_R.$
$(a, b) \notin R \Rightarrow [a]_R \cap [b]_R = \emptyset.$
$\bigcup\limits_{a \in A}[a]_R = A.$

Definition

The set of all equivalence classes of $R$ is the quotient set of $A$ w.r.t. $R$.

\[ A / R = \{[a]_R | a \in A\}. \]

Remark

If $A$ is finite, then $A / R$ is finite.
If $A$ has $n$ elements and each $[a]_R$ has $m$ elements, then $m | n$ and $A / R$ has $n / m$ elements.

Definition

A partition $\pi$ on a set $S$ is a family $\{A_1, A_2, \cdots, A_n\}$ of subsets of $S$ and

$\bigcup\limits_{k = 1}^{n} A_k = S.$
$A_j \cap A_k = \emptyset$ for every $j, k$ with $j \ne k$.

Theorem

Let $R$ be an equivalence relation on a set $S$, then the equivalence classes of $R$ form a partition of $X$.
Conversely, given a partition $\{A_i | i \in I\}$ of set $S$, there is an equivalence relation $R$ that has the set $A_i$ , $i \in I$ as its equivalence classes.

Partial Order¶

Definition

Relation $R_\preceq: S \leftrightarrow S$ is a partial order 偏序 if it's reflexive, antisymmetric and transitive.

A set $S$ together with a partial order $R_\preceq$ is called a partial order set or poset, denoted by $(S, R_\preceq)$.

Definition

$a, b \in (S, \preceq)$ are called comparable if either $a \preceq b$ or $b \preceq a$, otherwise incomparable.

If every elements of $(S, \preceq)$ are comaparable, then $S$ is called a totally order 全序 or linearly order set and $\preceq$ is called a total order or linear order. A totally ordered set is also called a chain.

Hasse Diagram¶

We can represent the partial order by a graph called Hasse Diagram. To construct a Hasse diagram, follow the steps below.

Start with the directed graph for the relation.
Remove all loops.
Remove the edges that must be present because of the transitivity.
Finally arrage each edges so that its inital vertex is below its terminal vertex, and remove all arrows.

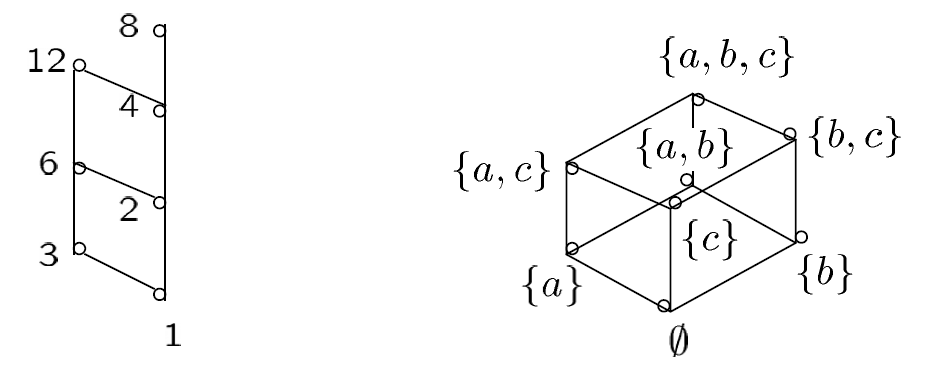
Example

Draw the Hasse diagram representing

the partial order $\{(a, b) | a \mid b\}$ on the set $\{1, 2, 3, 4, 6, 8, 12\}$.
the partial order $\{(A, B) | A \subseteq B\}$ on power set $2^S$, where $S = \{a, b, c\}$.

Maximial, Minimal, Greatest and Least Element¶

Definition

Let $(A, \preceq)$ be a partial ordered set, $B \subseteq A$.

$a$ is a maximal element 极大元 of $B$ if $a \in B \wedge \text{ There is no } x \in B \text{ s.t. } a \prec x$.
$b$ is a minimal element 极小元 of $B$ if $b \in B \wedge \text{ There is no } x \in B \text{ s.t. } x \prec b$.
$a$ is a the greatest element 最大元 of $B$ if $a \in B \wedge \forall\ x \in B, x \preceq a$.
$b$ is a the least element 最小元 of $B$ if $b \in B \wedge \forall\ x \in B, b \preceq x$.
$c$ is an upper bound 上界 of $B$ if $c \in A \wedge \forall\ x \in B : x \preceq c$.
$d$ is a lower bound 下界 of $B$ if $d \in A \wedge \forall\ x \in B : d \preceq x$.
$c$ is a least upper bound (lub) 上确界 of $B$ if $c$ is a upper bound and $\forall\ x$ is a upper bound, $c \preceq x$.
$d$ is a greatest lower bound (glb) 下确界 of $B$ if $d$ is a lower bound and $\forall\ x$ is a lower bound, $x \preceq d$.

Example

For $(A, \subseteq)$, where $A = 2^S$, $S = \{a, b, c, d\}$, consider the following concepts of $B = \{\emptyset, \{a\}, \{c\}, \{a, b\}\}$.

minimal element: $\emptyset$.
maximal element: $\{c\}, \{a,b\}$.
the greatest element: none.
the least element: $\emptyset$.
upper bound: $\{a, b, c\}, \{a, b, c, d\}$.
least upper bound: $\{a, b, c\}$.
lower bound: $\emptyset$.
least lower bound: $\emptyset$.

Lattice¶

Definition

A partially ordered set in which every pair of elements has both a least upper bound and a greatest lower bound is called a lattice 格.

Example

The poset $(\mathbb{Z}, \mid)$ is a lattice, since for the pair $(a, b)$, $\text{lub}(a, b) = \text{lcm}(a, b)$ and $\text{glb}(a, b) = \text{gcd}(a, b)$.
The poset $(\{1, 2, 3, 4, 5\}, \mid)$ is not a lattice, since $\text{lub}(2, 3) = \text{lcm}(2, 3) = 6 \notin \{1, 2, 3, 4, 5\}$.

最后更新: 2023.11.21 17:00:13 CST
创建日期: 2022.11.10 01:04:43 CST