概率论与数理统计

Warning

It's not a complete note, but a simple review of concepts and most of the concerned formulae.

Since this course is taught and examined in Chinese, I write in Chinese there.

1 概率论的基本概念

1.1 样本空间与随机事件

• 随机试验，样本空间，样本点，随机事件，基本事件，必然事件，不可能事件
• 事件的关系
  • 包含、相等、和事件、积事件、逆事件、差事件
  • 互不相容/互斥
• 交换律、结合律、分配律、德摩根律
• 并联系统、串联系统

1.2 频率和概率

• 频率，概率

• 定义

  • 非负性 \(P(A) \ge 0\)
  • 规范性 \(P(S) = 1\)

  • 可列可加性

    \[ P\left(\bigcup_{j = 1}^{\infty} A_j \right) = \sum\limits_{j = 1}^{\infty} P(A_j). \]

• 性质

  • 有限可加性

    \[ P\left(\bigcup_{j = 1}^{n} A_j \right) = \sum\limits_{j = 1}^{n} P(A_j). \]

  • \(P(A) = 1 - P(\overline{A})\)

  • 当 \(B \subset A\), \(P(A - B) = P(A) - P(B)\), \(P(A) \ge P(B)\).
  • 容斥原理 \(P(A \cup B) = P(A) + P(B) - P(AB)\).
  • \(P(B | A) = \dfrac{P(AB)}{P(A)}\).

1.3 等可能概型

1.4 条件概率

• 条件概率
• 全概率公式 - \(P(A) = \sum\limits_{j = 1}^{n} P(B_j) P(A|B_j)\) - \(P(A|C) = \sum\limits_{j = 1}^{n} P(AB_j | C) = \sum\limits_{j = 1}^{n} P(B_j | C) \cdot P(A| B_jC)\)

• 贝叶斯公式 Bayes Formula

  \[ P(B_i | A) = \frac{P(B_i)P(A|B_i)}{\sum\limits_{j = 1}^{n}P(B_j)P(A|B_j)} \]
  • 先验概率，后验概率

1.5 事件的独立性与独立试验

• 相互独立，两两独立，相互独立比两两独立强
• 条件独立

2 随机变量及其概率分布

2.1 随机变量

• 随机变量

2.2 离散型随机变量

• 离散型随机变量，离散型分布
• 概率分布律
• 常见分布
  • 0 - 1 分布 / 两点分布 \(0-1(p)\) 伯努利试验
    • \(P(X = k) = p^k(1 - p)^{1 - k}\)
    • \(E(X) = p\)
  • 二项分布 \(B(n,p)\) n 重伯努利试验
    • \(P(X = k)=C^k_n p^k(1 - p)^{n - k}\)
    • \(E(X) = np\)
    • \(D(X) = np(1 - p)\)
  • 泊松分布 \(P(\lambda)\)
    • \(P(X = k)=\dfrac{e^{-\lambda} \lambda^k}{k!}\)
    • 拟合二项分布，\(\lambda=np\)
    • \(E(X) = \lambda\)
    • \(D(X) = \lambda\)
  • 几何分布 \(\text{Geom}(p)\)
    • \(P(X = k) = p(1 - p)^{k - 1}\)
    • 无记忆性
    • \(E(X) = \dfrac{1}{p}\)
    • \(D(X) = \dfrac{1 - p}{p^2}\)
  • 超几何分布 \(H(n, a, N)\)
    • \(P(X = k) = \dfrac{C_a^k C_b^{n-k}}{C_N^n},\ \ a + b = N\)
    • \(E(X) = n \dfrac{a}{N}\)
    • \(D(X) = n \dfrac{a(N - a)(N - n)}{N^2(N - 1)}\)
  • 巴斯卡分布 \(NB(r, p)\)
    • \(P(X = k) = C_{k - 1}^{r - 1} p^r (1 - p)^{k - r}\)

2.3 随机变量的概率分布函数

• 分布函数 \(F(x) = P(X \le x)\)
• 性质：单调不减；无限处极限；右连续 \(F(x) = F(x + 0)\) （左闭右开）

2.4 连续型随机变量

• 连续型随机变量，概率密度函数(p.d.f.)，支撑

• \(F(x) = \int_{-\infty}^x f(t)dt\).

• 常见分布

  • 均匀分布 \(U(a,b)\)
    • \(f(x)=\left\{ \begin{array}{l} \dfrac{1}{b-a}, & x \in (a, b), \\ 0, & \text{else}. \end{array} \right.\)
    • \(F(x)=\left\{ \begin{array}{l} 0, & x < a, \\ \dfrac{x - a}{b - a}, & x \in (a, b), \\ 1, & \text{else}. \end{array} \right.\)
    • \(E(X) = \dfrac{a + b}{2}\)
    • \(D(X) = \dfrac{(b - a)^2}{12}\)
  • 正态分布 \(N(\mu, \sigma^2)\)
    • \(f(x) = \dfrac{1}{\sqrt{2 \pi}\sigma} e^{-(x - \mu)^2 / (2 \sigma^2)}\)
    • \(F(x) = \int_{-\infty}^{x} \dfrac{1}{\sqrt{2 \pi} \sigma} e^{-(t - \mu)^2 / (2 \sigma^2)} dt\)
    • \(E(X) = \mu\)
    • \(D(X) = \sigma^2\)
  • 指数分布 \(E(\lambda)\)
    • \(f(x)=\left\{ \begin{array}{l} \lambda e^{-\lambda x}, & x > 0, \\ 0, & \text{else}. \end{array} \right.\)
    • \(F(x)=\left\{ \begin{array}{l} 1 - e^{-\lambda x}, & x > 0, \\ 1, & \text{else}. \end{array} \right.\)
    • 无记忆性 \(P(X > t_0 + t | X > t_0) = P(X > t)\)
    • \(E(X) = \dfrac{1}{\lambda}\)
    • \(D(X) = \dfrac{1}{\lambda^2}\)

2.5 随机变量函数的分布

• 可加性
  • \(X \sim B(n, p),\ \ Y \sim B(m, p) \Rightarrow X + Y \sim B(m + n, p)\)
  • \(X \sim P(\lambda_1),\ \ Y \sim P(\lambda_2) \Rightarrow X + Y \sim P(\lambda_1 + \lambda_2)\)
  • \(X\sim N(\mu_1,\sigma_1^2),Y\sim N(\mu_2,\sigma_2^2) \Rightarrow X\pm Y\sim N(\mu_1 \pm \mu_2,\sigma_1^2+\sigma_2^2)\)

3 多元随机变量及其分布

3.1 二元离散型随机变量

• 联合概率分布律 / 联合分布律，边际分布律，条件分布律

3.2 二元随机变量的分布函数

• 联合概率分布函数 / 联合分布函数，边际分布函数，条件分布函数

3.3 二元连续型随机变量

• 联合概率密度函数 / 联合密度函数，边际密度函数，条件密度函数
• \(F(x,y) = P(X\le x, Y\le y)\)
• \(F_{X|Y}(x|y) = \dfrac{P(X \le x, Y = y)}{P(Y = y)} = \lim\limits_{\Delta y \rightarrow 0^+}\dfrac{P(X \le x, y < Y \le y + \Delta y)}{P(y < Y \le y + \Delta y)}\)
• \(f_X(x) = \int_{-\infty}^{\infty}f(x,y)dy\)
• \(f_{X|Y}(x|y) = \dfrac{f(x, y)}{f_Y(y)},\ \ f(x, y) = f_Y(y)f_{X|Y}(x|y)\)
• \(F_{X|Y}(x|y) = P(X \le x | Y = y) = \int_{-\infty}^x f_{X|Y}(x|y)dx\)
• 常见分布
  • 均匀分布
  • 正态分布 \(X, Y \sim N(\mu_1, \mu_2; \sigma_1^2, \sigma_2^2; \rho)\)
    • \(X \sim N(\mu_1, \sigma_1^2),\ \ Y \sim N(\mu_2, \sigma_2^2)\)

3.4 随机变量的独立性

• \(X,Y\) 独立时，\(P(X\le x,Y\le y) = P(X\le x) \cdot P(Y\le y)\), 即 \(F(x, y) = F_X(x) F_Y(y)\)
• 对于连续型随机变量，充要条件是 \(f(x, y) = m(x)n(y)\)

3.5 二元随机变量函数的分布

• \(Z = X + Y\)
  • \(P(Z = z) = P(X + Y = z) = \sum\limits_{i = 1}^{+\infty} P(X = x_i, Y = z - x_i)\)
  • \(f_Z(z) = \int_{-\infty}^{+\infty} f(x, z - x) dx \overset{独立}{=\!=\!=} \int_{-\infty}^{+\infty} f_X(x) f_Y(z - x)dx\)
• \(M = \max(X_1, X_2, \dots, X_N),\ \ N = \min(X_1, X_2, \dots, X_N)\)
  • 相互独立: \(F_{M}(z) = \prod\limits_{i = 1}^{n} F_i(t),\ \ F_{N} = 1 - \prod\limits_{i = 1}^{n} [1 - F_i(t)]\)

4 随机变量的数字特征

4.1 数学期望

• 定义，存在性，性质
• \(E(X) = \sum\limits_{k = 1}^{+\infty} x_k p_k = \int_{-\infty}^{\infty}xf(x)dx\)
• \(E(Y) = E(g(X)) = \sum\limits_{k = 1}^{+\infty} g(x_k) p_k = \int_{-\infty}^{+\infty}g(x)f(x)dx\)
• \(E(Z) = E(h(X, Z)) = \sum\limits_{i = 1}^{+\infty} \sum\limits_{j = 1}^{+\infty} h(x_i, y_j) p_{ij} = \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}h(x, y)f(x,y)dxdy\)
• 性质
  • \(E(C) = C\)
  • \(E(CX) = C \cdot E(X)\)
  • \(E(X + Y) = E(X) + E(Y)\)
  • 相互独立，\(E(XY) = E(X)E(Y)\)

4.2 方差、变异系数

• 方差，标准差
• \(\text{Var}(X), D(X), V(X)\)
• \(\text{Var}(X) = E[(X -E(X))^2]\)
• \(\text{Var}(X) = E(X^2)-(E(X))^2\)
• 性质
  • \(\text{Var}(C) = 0\)
  • \(\text{Var}(CX) = C^2 \cdot \text{Var}(X)\)
  • \(\text{Var}(X + Y) = \text{Var}(X) + \text{Var}(Y) + 2\text{Cov}(X, Y)\)
  • \(\text{Var}(X) = 0 \Leftrightarrow P(X = C) = 1 \wedge C = E(X)\)
• 标准化随机变量
  • \(X^*=\dfrac{X - E(X)}{\sqrt{\text{Var}(X)}}\)
• 变异系数
  • \(C_v(X) = \dfrac{\sqrt{\text{Var}(X)}}{E(X)}\)

4.3 协方差与相关系数

• 协方差
  • \(\text{Cov}(X, Y) = E[(X - E(X))(Y - E(Y))]\)
  • \(\text{Cov}(X, Y) = E(XY)-E(X)E(Y)\)
• 性质
  • \(\text{Cov}(X, Y) = \text{Cov}(Y, X)\)
  • \(\text{Cov}(X, X) = \text{Var}(X)\)
  • \(\text{Cov}(aX, bY) = ab \cdot \text{Cov}(X, Y)\)
  • \(\text{Cov}(X_1 + X_2) = \text{Cov}(X_1, Y) + \text{Cov}(X_2, Y)\)
• 相关系数
  • \(\rho_{XY}=\dfrac{\text{Cov}(X,Y)}{\sqrt{\text{Var}(X)}\sqrt{\text{Var}(Y)}} = \text{Cov}(X^*, Y^*) \in [-1,1]\)
  • 大于一正相关，小于一负相关，零则不相关
  • 不相关等价条件
    • \(\text{Cov}(X, Y) = 0\)
    • \(E(XY) = E(X)E(Y)\)
    • \(\text{Var}(X + Y) = \text{Var}(X) + \text{Var}(Y)\)
    • 相互独立是不相关的充分条件

4.4 其他数字特征

• 矩
  • \(k\) 阶原点矩 \(E(X^k)\)
  • \(k\) 阶中心矩 \(E([X - E(X)]^k)\)
  • \(k + l\) 阶混合原点矩 \(E(X^k Y^l)\)
  • \(k + l\) 阶混合中心矩 \(E([X - E(X)]^k [Y - E(Y)]^l)\)

4.5 多元随机变量的数字特征

• 多元随机变量的数字特征
  • 对于 \(\vec{X}=(X_1,X_2,\cdots,X_n)^T,X_i\sim N(\mu_i,\sigma_i)\)，\(\vec{X}\sim N(\vec{a},\vec{B})\)
  • 当 \(n=2,\ \ \vec{B}=\begin{bmatrix} \sigma_1^2&\sigma_1\sigma_2\rho\\ \sigma_1\sigma_2\rho&\sigma_2^2 \end{bmatrix}\)

5 大数定律及中心极限定理

5.1 大数定律

• 依概率收敛

  • \(\forall\ \varepsilon \gt 0,\ \ \lim\limits_{x \rightarrow +\infty}P(|Y_n-c|\ge\varepsilon)=0\)
  • \(Y_n\stackrel{P}\longrightarrow c,\ \ n\rightarrow +\infty\)

  • \(n\rightarrow +\infty,\ \ X_n\stackrel{P}\longrightarrow a,\ \ Y_n\stackrel{P}\longrightarrow b\), \(g(x, y)\) 在 \((a, b)\) 连续，

    \[ g(X_n, Y_n)\stackrel{P}\longrightarrow g(a, b),\ \ n\rightarrow +\infty \]

• 马尔可夫不等式

  \[ P(|Y| \ge \varepsilon) \le \dfrac{E(|Y|^k)}{\varepsilon^k} \]

• 切比雪夫不等式

  \[ P(|X-\mu| \ge \varepsilon) \le \dfrac{\sigma^2}{\varepsilon^2} \]

• 大数定律

  • 设 \(\{Y_i\}\) 为一随机变量序列，存在常数序列 \(\{c_n\}\) 使得，

    \[ \lim\limits_{n\rightarrow +\infty} P \left(\left|\frac{1}{n}\sum\limits_{i=1}^nY_i-c_n\right|\ge\varepsilon\right)=0 \]

  • \(n\rightarrow+\infty,\ \ \dfrac{1}{n}\sum\limits_{i=1}^nY_i-c_n\stackrel{P}\longrightarrow0\)

  • 特别地，当 \(c_n=c\)，可写为 \(n\rightarrow+\infty,\ \ \dfrac{1}{n}\sum\limits_{i=1}^nY_i\stackrel{P}\longrightarrow c\)

• 伯努利大数定律

  \[ \lim_{n\rightarrow+\infty} P \left(\left|\dfrac{n_A}{n}-p\right|\ge\varepsilon\right)=0 \]

• 辛钦大数定律（独立同分布）

  \[ \lim_{n\rightarrow+\infty} P \left(\left|\frac{1}{n}\sum_{i=1}^nX_i-\mu\right|\ge\varepsilon\right)=0 \]
  • 推论
  \[ \lim_{n\rightarrow+\infty} P \left(\left|\frac{1}{n}\sum_{i=1}^n h(X_i) - E(h(X_1)) \right| \ge \varepsilon\right) = 0 \]

5.2 中心极限定理

独立同分布

• 林德伯格-莱维中心极限定理

  \[ \lim\limits_{n\rightarrow+\infty}P\left(\dfrac{\sum\limits_{i=1}^nX_i-E(\sum\limits_{i=1}^nX_i)}{\sqrt{\text{Var}\left(\sum\limits_{i=1}^nX_i\right)}}\le x\right) = \lim\limits_{n\rightarrow+\infty} P \left(\dfrac{\sum\limits_{i=1}^nX_i-n\mu}{\sigma\sqrt{n}}\le x \right) =\Phi(x) \]

• 棣莫弗-拉普拉斯中心极限定理

  \[ \lim\limits_{n\rightarrow+\infty} P \left(\dfrac{n_A-np}{\sqrt{np(1-p)}}\le x \right) = \Phi(x) \]

6 统计量与抽样分布

6.1 随机样本与统计量

• 总体、个体、有限总体、无限总体

• 抽样、样本（代表性、独立性）、样本容量、随机样本

• 统计量：样本均值，样本方差，样本 \(k\) 阶原点矩，样本 \(k\) 阶中心矩

• 样本均值

  \[ \overline{X} = \frac{1}{n} \sum\limits_{i = 1}^{n} X_i \]

• 样本方差

  \[ S^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})=\frac{1}{n-1}\left(\sum_{i=1}^nX_i^2-n\overline{X}^2\right) \]

• 样本 \(k\) 阶（原点）矩

  \[ A_k=\frac{1}{n}\sum_{i=1}^nX_i^k \]

• 样本 \(k\) 阶中心矩

  \[ B_k=\frac{1}{n}\sum_{i=1}^n(X_i-\overline{X})^k \]

6.2 \(\chi^2\) 分布，\(t\) 分布，\(F\) 分布

• \(\chi^2\) 分布
  • \(\chi^2(n) = \sum\limits_{i = 1}^{n} X_i^2,\ \ X_i \sim N(0, 1)\)
  • \(X, Y\) 相互独立, \(X \sim \chi^2(m),\ \ Y \sim \chi^2(n) \Rightarrow X + Y \sim \chi^2(m + n)\)
  • \(E(\chi^2(n)) = n\)
  • \(D(\chi^2(n)) = 2n\)
  • \(n > 40\), \(\chi^2_\alpha(n) \approx \dfrac{1}{2}(z_\alpha + \sqrt{2n - 1})^2\)
• \(t\) 分布
  • \(t(n) = \dfrac{X}{\sqrt{Y / n}},\ \ X \sim N(0, 1),\ \ Y \sim \chi^2(n)\)
  • \(n \rightarrow +\infty,\ \ t(n) \rightarrow N(0, 1)\)
  • \(E(T) = 0,\ \ n \ge 2\)
  • \(D(T) = \dfrac{n}{n - 1},\ \ n \ge 3\)
  • \(n > 45,\ \ t_\alpha (n) \approx z_\alpha\)
• \(F\) 分布
  • \(F(n_1, n_2) = \dfrac{U / n_1}{V / n_2}\)
  • \(F \sim F(n_1, n_2) \Rightarrow \dfrac{1}{F} \sim F(n_2, n_1)\)
  • \(F_{1 - \alpha}(n_1, n_2) = \dfrac{1}{F_\alpha(n_2, n_1)}\)

6.3 正态总体下抽样分布

• \(E(\overline{X}) = \mu, \ \ \text{Var}(\overline{X}) = \dfrac{\sigma^2}{n}\)
• \(E(S^2) = \sigma^2,\ \ E(B_2) = \dfrac{n - 1}{n} \sigma^2\)
• 正态总体下
  • \(\overline{X}\sim N(\mu,\dfrac{\sigma^2}{n})\)
  • \(\text{Var}(S^2) = \dfrac{2\sigma^4}{n - 1}\)
  • \(\dfrac{\sum\limits_{i = 1}^{n} (X_i - \overline{X})^2}{\sigma^2} = \dfrac{(n- 1) S^2}{\sigma^2}\sim\chi^2(n-1)\)
  • \(\overline{X}\) 与 \(S^2\) 相互独立
  • \(\dfrac{\overline{X} - \mu}{S / \sqrt{n}} \sim t(n - 1)\)
  • \(\dfrac{S_1^2 / \sigma_1^2}{S_2^2 / \sigma_2^2} \sim F(n_1 - 1, n_2 - 1)\)
  • \(\dfrac{(\overline{X} - \overline{Y}) - (\mu_1 - \mu_2)}{\sqrt{\dfrac{\sigma_1^2}{n_1^2} + \dfrac{\sigma_2^2}{n_2}}} \sim N(0, 1)\)
  • \(\sigma_1^2 = \sigma_2^2 = \sigma,\ \ \dfrac{(\overline{X} - \overline{Y}) - (\mu_1 - \mu_2)}{S_w\sqrt{\dfrac{1}{n_1^2} + \dfrac{1}{n_2}}} \sim t(n_1 + n_2 - 2),\ \ S_w^2 = \dfrac{(n_1 - 1)S_1^2 + (n_2 - 1) S_2^2}{n_1 + n_2 - 2}\)

7 参数估计

点估计

• 矩法
  • 用矩表示统计量，再用 \(A_k \rightarrow \mu_k,\ \ B_k \rightarrow \nu_k\) 替换
• 极大似然法
  • \(L(\theta) = \prod\limits_{i = 1}^n f(x_i; \theta)\)
  • \(L(\hat \theta) = \max\limits_{\theta \in \Theta} L(\theta). \left(\left.\dfrac{dL(\theta)}{d\theta}\right|_{\theta = \hat{\theta}} = 0\right)\)
  • 为了计算方便，取对数 \(l(\theta)=\ln L(\theta)\).

评价准则

• 无偏性准则
  • 无偏估计 \(E(\hat{\theta})=\theta\).
  • 渐近无偏估计 \(\lim\limits_{n\rightarrow+\infty}E(\hat{\theta})=\theta\).
• 有效性准则
  • 方差 \(\text{Var}(\theta)\)
  • 方差越小越有效.
• 均方误差准则
  • 均方误差 \(\text{Mse}(\hat{\theta})=E[(\hat{\theta}-\theta)^2]\).
  • 均方误差越小越有效.
• 相合性准则
  • \(\lim\limits_{n\rightarrow+\infty} P (|\hat{\theta}_n-\theta|<\varepsilon)=1,\ \ \hat{\theta}_n\stackrel{P}\longrightarrow\theta\) 则称为相合估计量.

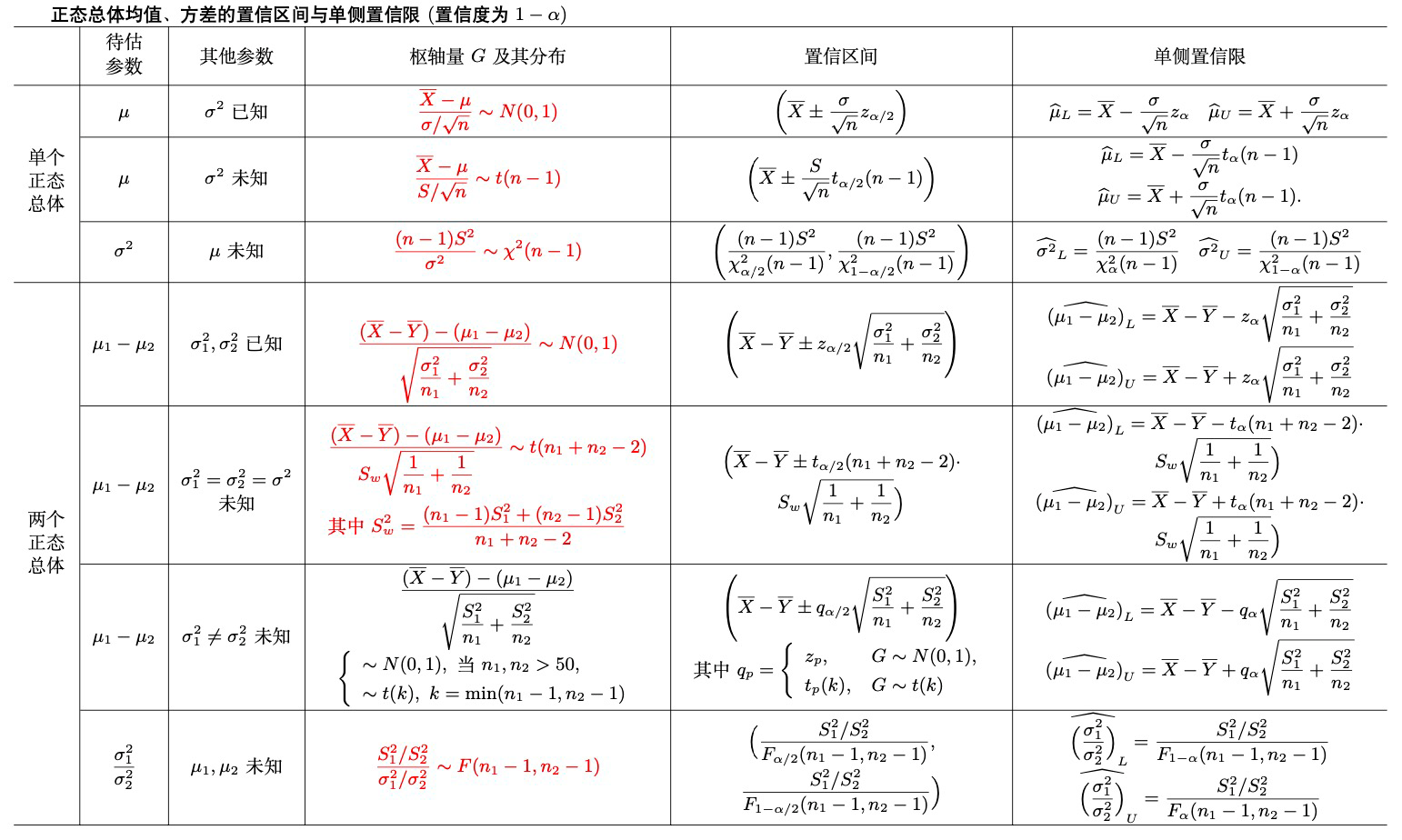
区间估计

• 正态总体

• 非正态总体

  • 0 - 1 分布

    \[ P\left(-z_{\alpha/2}<\frac{n\overline{X}-np}{\sqrt{np(1-p)}}<z_{\alpha/2}\right)\approx 1-\alpha \]

  • 其他分布均值为 \(\mu\)

    \[ \frac{\sum\limits_{i=1}^nX_i-n\mu}{\sqrt{n}\sigma}\sim N(0,1) \]

    \(\left(\overline{X}\pm\dfrac{\sigma}{\sqrt{n}}z_{\alpha/2}\right)\)，\(\sigma^2\) 未知时使用 \(S^2\) 替代.

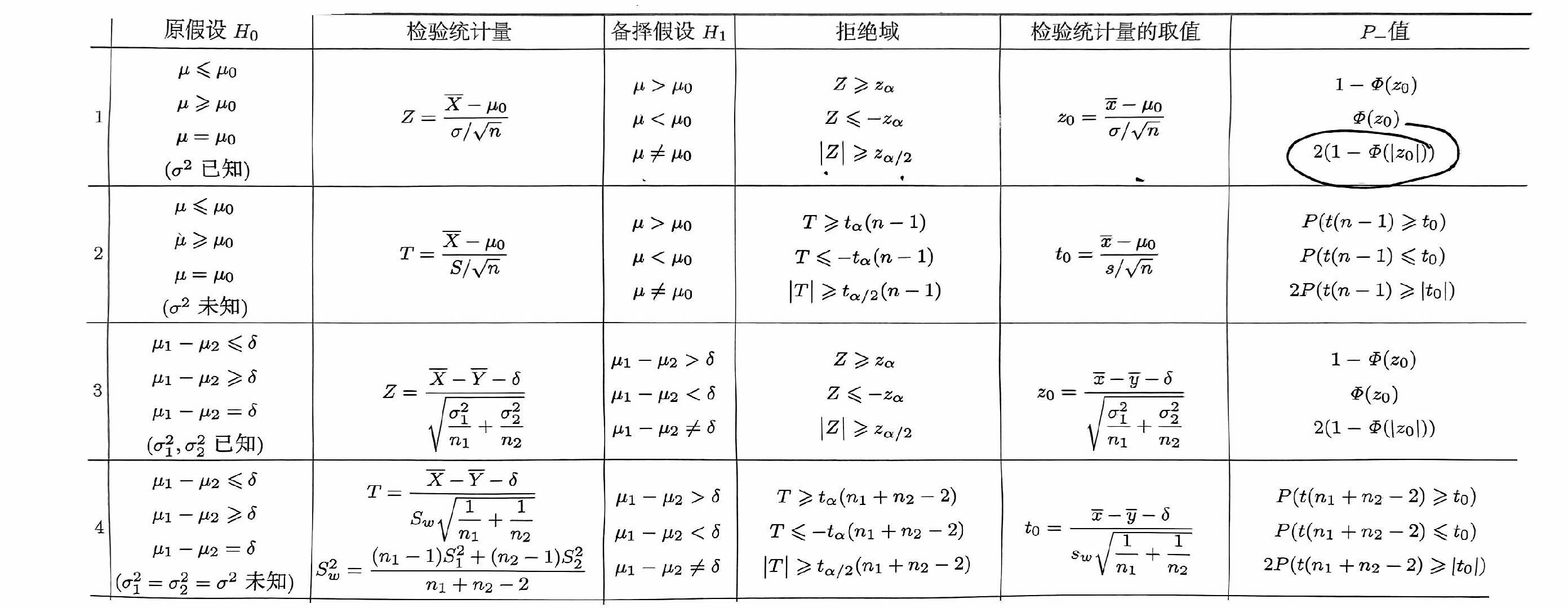
8 假设检验

• 原假设，备择假设
• 检验，接收域，拒绝域，检验统计量
• 第一类错误（弃真），第二类错误（取伪）
• 显著性水平

---

最后更新: 2023.11.21 17:00:13 CST
创建日期: 2023.02.22 01:24:06 CST