Disjoint Set¶

Definition (Recap)

A relation $R$ is defined on a set $S$ if for every pair of elements $(a, b)$, $a, b \in S$, $aRb$ is either true of false. If $aRb$ is true, then $a$ is related to $b$.

A relation $\sim$ over a set $S$ is said to be an equivalence relation over $S$ iff it's symmetric, reflexive and transitive over $S$.

Two members $x$ and $y$ of a set $S$ are said to be in the same equivalence class iff $x \sim y$.

ADT

Objects:

Elements of the sets: $1, 2, 3, \dots, N$.
Disjoint sets: $S_1, S_2, \dots$.

Operations:

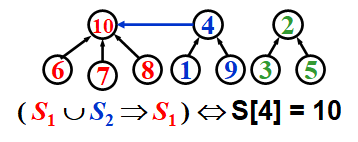
Union two sets $S_i$ and $S_j$ to $S$, i.e. $S = S_i \cup S_j$.
Find the set $S_k$ which contains the element $i$.

Implementation¶

Method 1 | Tree¶

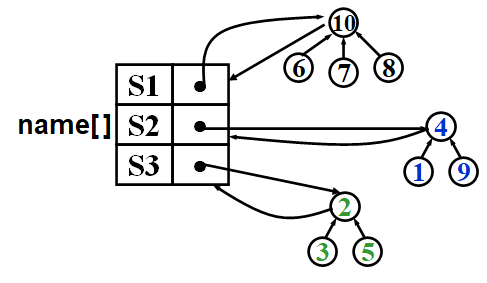
The sets is represented by a forest. Each set $S_i$ is represented by a tree, and the root of the tree is the representation element. And a list name stores the roots of the trees.

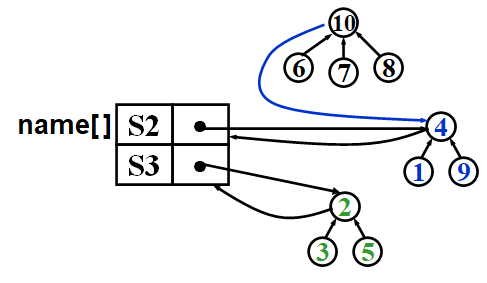
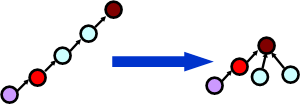
For Union operation, it sets the parent of the root of one tree to the other root. The following picture shows

\[ S_2 \cup S1 \Rightarrow S_2. \]

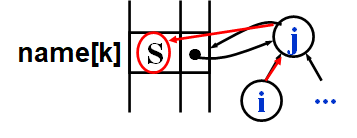
For Find operation, it finds the root of $i$ and its corresponding name, which is 'S' in the following picture.

Method 2 | Array¶

Another method is to maintain an array $S$ of size $N$ to reprsent the trees in Method 1.

\[ S[\text{element}] = \left\{ \begin{aligned} & 0, && \text{if the element is root}, \\ & \text{the element's parent}, && \text{if the element isn't root}. \end{aligned} \right. \]

And the name of each set is the index of the root.

For Union operation, we just set

S[root_2] = root_1.

For Find operation, we iteratively or recursively find its parent until S[x] = 0.

while (S[x] > 0) {
    x = s[x];
}
return x;

Improvement¶

Motivation: There may be the case that a sequence of special operations that makes the tree degenerate to a list.

Heuristic Union Stategy¶

Union-by-Size¶

When union two sets $S_1$ and $S_2$ (represented by trees), if the size of $S_1$ is smaller, then we union $S_1$ to $S_2$.

To indicate the size of a set, suppose we only consider the positive indices, we can let S[root] = -size (initialized with -1) instead of S[root] = 0.

Union by Size

void Union(int *S, const int root_a, const int root_b) {
    if (root_a < root_b) {
        S[root_a] += S[root_b];
        S[root_b] = root_a;
    } else {
        S[root_b] += S[root_a];
        S[root_a] = root_b;
    }
}

Proposition

Let $T$ be a tree created by union-by-size with $N$ nodes, then

\[ \text{height}(T) \le \lfloor \log_2N \rfloor. \]

Time complexity of $N$ Union and $M$ Find operations is now $O(N + M\log_2N)$.

Union-by-Height / Rank¶

When union two sets $S_1$ and $S_2$ (represented by trees), if the height of tree $S_1$ is smaller, then we union $S_1$ to $S_2$.

The height of a tree increases only when two equally deep trees are joined (and then the height goes up by one).

Union by Height

void Union(int *S, const int root_a, const int root_b) {
    if (S[root_a] > S[root_b]) {
        S[root_a] = root_b;
        return;
    }
    if (S[root_a] < S[root_b]) {
        S[root_b] = root_a;
        return;
    }
    S[root_a] --;
    S[root_b] = root_a;
}

Path Compression¶

When we are finding an element, we can simultaneously change the parents of the nodes along the finding path, including itself, to the root, which makes the tree shallower.

When finding the root of the **purple** node

Union-Find / Disjoint Set

int *Initialize(const int n) {
    int *S = (int *)malloc(n * sizeof(int));
    for (int i = 0; i < n; ++ i) {
        S[i] = -1;
    }
    return S;
}

int Find(int *S, const int a) {
    if (S[a] < 0) {
        return a;
    }
    return S[a] = Find(S, S[a]);
}

void Union(int *S, const int root_a, const int root_b) {
    if (root_a < root_b) {
        S[root_a] += S[root_b];
        S[root_b] = root_a;
    } else {
        S[root_b] += S[root_a];
        S[root_a] = root_b;
    }
}

Time Complexity¶

After heuristic union (union-by-rank) and path compression, the average time complexity of each operation is

\[ O(\alpha(n)),\ \ \text{ where $\alpha$ is the inverse function of Ackermann function}. \]

Its growth is very slow, which can be regarded as a constant.

Ackermann function $A(m,n) $ is defined by

\[ A(i, j) = \left\{ \begin{aligned} & 2^j, && i = 1 \text{ and } j \ge 1 \\ & A(i - 1, 2), && i \ge 2 \text{ and } j = 1 \\ & A(i - 1, A(i, j - 1)), && i \ge 2 \text{ and } j \ge 2 \\ \end{aligned} \right. \]

and $\alpha(n)$ is defined by the maximum $m$ s.t. $A(m, m) \le n$. $\alpha(n) = O(log^* n)$ (iterative logarithm).

Iterative Logarithm

\[ \log^* n = \left\{ \begin{aligned} & 0, && \text{if } n \le 1 \\ & 1 + \log^*(\log_2 n). && \text{if } n > 1 \\ \end{aligned} \right. \]

Thus we have

\[ \begin{aligned} \log^* 2 &= 1 + \log^*(\log_2 2) = 1 + \log^*1 = 1, \\ \log^* 4 &= 1 + \log^*(\log_2 4) = 1 + \log^*2 = 2, \\ \log^* 16 &= 1 + \log^*(\log_2 16) = 1 + \log^*4 = 3, \\ \log^* 65536 &= 1 + \log^*(\log_2 65536) = 1 + \log^*16 = 4, \\ \log^* 2^{65536} &= 1 + \log^*(\log_2 2^{65536}) = 1 + \log^*65536 = 5. \\ \end{aligned} \]

Improvement	Average Time Complexity	Worst Time Complexity
No improvement	$O(\log n)$	$O(n)$
Path Compression	$O(\alpha (n))$	$O(\log n)$
Union by Rank	$O(\log n)$	$O(\log n)$
Both	$O(\alpha(n))$	$O(\alpha(n))$

最后更新: 2023.11.21 17:00:13 CST
创建日期: 2022.11.10 01:04:43 CST

Improvement	Average Time Complexity	Worst Time Complexity
No improvement	\(O(\log n)\)	\(O(n)\)
Path Compression	\(O(\alpha (n))\)	\(O(\log n)\)
Union by Rank	\(O(\log n)\)	\(O(\log n)\)
Both	\(O(\alpha(n))\)	\(O(\alpha(n))\)